63 Анализ стоимости денег и дисконтирования

Принцип стоимости денег во времени (time value of money), который является краеугольным камнем в современном финансовом менеджменте, гласит: «сегодняшние поступления являются ценными от будущих» Стоимость денег во времени изменяется с учетом нормы доходности на денежном рынке и рынке ЦБ Как норма доходности может выступать норма ссудного процента или норма выплаты дивидендов по обыкновенным и привилегированным ими акциями.

Из принципа стоимости денег следует два важных наcлидкы:

• необходимость учета фактора времени при проведении финансовых операций;
• некорректность (с точки зрения анализа долгосрочных финансовых операций) простого добавления денежных величин, касающихся различных периодов времени

Учет стоимости денег во времени является определяющим при анализе целесообразности инвестиций в ценные бумаги, поскольку игнорирование этого фактора может привести к ошибочным инвестиционных решений

Анализ фактора времени при проведении финансовых операций требует применения специальных методов его оценки Это так называемые метод приращение (compounding) и метод дисконтирования (discounting), которые играют важную роль в финансовом анализе, поскольку позволяют сопоставить стоимости потоков платежей (cash flows) С помощью методов приращение и дисконтирования, основанные на технике процентных вычислений, осуществляется приведение денежных сумм, относящихся к различным временным периодам, к нужному момент ту времени в настоящем или будущем При этом как норма приведения используется процентная ставка r (interest ratee).

Метод приращение позволяет определить будущую величину (future value - FV) текущей суммы (present value - PV) через некоторый промежуток времени, исходя из заданной процентной ставки r

Дисконтирование представляет собой процесс нахождения оцениваемой величины в определенный момент времени по ее известному или предполагаемым значением в будущем

В экономическом смысле величина PV, определенная дисконтированием, показывает текущее значение будущей величины FV

Как правило, в краткосрочных финансовых операциях, срок проведения которых меньше года, используются простые проценты Базой для исчисления процентов за каждый период в этом случае является первоначальная (начальная) сумма сделки При анализе долгосрочных инвестиционных вложений используются сложные процентыки.

Для простых процентов приращение определяется по формуле:

соответствии дисконтирования - по формуле:

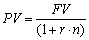
где FV - будущая стоимость (величина);

PV - текущая стоимость;

n - число периодов дисконтирования;

r - процентная ставка

число периодов дисконтирования в приведенных формулах иногда заменяется:

где t - длительность проведения операции в днях;

B - временная база (число дней в году: 360, 365 или 366, определяется действующими нормативными документами и учетной политикой эмитента) Поскольку формулы простых процентов используются только для я оценки краткосрочных вложений, то, очевидно, всегда t \u003c36 365.

Обычно при определении продолжительности проведения операции даты ее начала и окончания считаются за один день (учитывается дата начала и не учитывается дата ее окончания) В зависимости от параметров в t и B, возможны следующие варианты начисления процентов:

• 365/365 - точное число дней проведения операции и фактическое количество дней в году;
• 365/360 - точное число дней проведения операции и финансовый год (12 месяцев по 30 дней);
• 360/360 - приближенное число дней проведения операции (месяц принимается равным 30-ти дням) и финансовый год (12 месяцев по 30 дней)

Для оценки стоимости долгосрочных финансовых инвестиций используют сложные проценты Будущая стоимость денег с использованием сложных процентов (приращение) составляет:

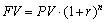
где PV - текущая стоимость;

FV - будущая стоимость;

n - количество периодов времени, на которую производится вложения;

r - процентная ставка

Текущее (современное) значение стоимости определенной будущей суммы денег определяется с помощью формулы дисконтирования с аналогичными обозначениями:

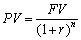
Степенная зависимость в формулах связана с особенностями начисления сложных процентов, когда сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход При этом база для начисления процентов за следующий период включает в себя как первоначальную сумму инвестиции, так и сумму уже нако Пичено ранее процентныев.

Пример 2 Пусть инвестор покупает учетную облигацию номинальной стоимостью 2000 грн с погашением через два года Какая разумная цена облигации, если депозитная процентная ставка составляет сегодня 15% ре ичныхрічних?

С помощью формулы с использованием сложных процентов

PV = FV / (1 r) n

легко определить, что текущая стоимость суммы погашения (номинальной стоимости) составляет:

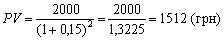
Размер r интерпретируется в формуле дисконтирования как ставка дисконтирования и часто называется просто дисконтом.

Задача определения ставки дисконтирования является важным для выполнения соответствующих финансово-экономических расчетов, прежде всего при оценке эффективности инвестиций часто этот коэффициент берется без с всякого обоснования как наиболее типичный или распространенный или определяется уровнем доходности одного из самых популярных рыночных инструментов (например, доходность по банковским депозитам аб в ставка по банковским кредитам).

Объект инвестирования будет привлекательным для инвестора, если его норма доходности будет превышать таковую для любого иного способа вложения средств с аналогичным риском Итак, ставка дисконтирования ния, используемый для расчетов, должна отражать требуемую норму доходности для данного инвестиционного проекта.

Ставка дисконтирования должна учитывать минимально гарантированный уровень доходности (не зависит от вида инвестиционных вложений), темп инфляции и коэффициент, учитывающий степень риска у конкретного инвестирования есть этот показатель отражает минимально допустимую отдачу на вложенный капитал (при которой инвестор предпочтет участие в проекте, альтернативном вложению тех же к оштив в другой проект с сопоставимой степенью риска).

Практическое применение инструмента дисконтирования при принятии инвестиционных решений рассмотрим на примере выбора инвестором одного из трех объектов инвестирования - процентных облигаций номи альной стоимостью 10 000,00 грн со сроком обращения два года (при условии, что показателем дисконтирования выбирается текущая ставка межбанковского кредитования 12,0% годовых) с различными условиями выпускамовами випуску:

а) с номинальной доходностью 20,0% годовых и ежеквартальной выплатой процентов;

б) с номинальной доходностью 20,4% годовых и ежегодной уплатой процентов;

в) с номинальной доходностью 22,0% годовых и уплатой процентов при погашении

Поскольку периодичность и суммы процентных выплат отличаются, данные по номинальной и дисконтированной стоимости процентных выплат по каждому из вариантов для удобства сравнения сведем в табл 64 4 При годовой ставке r = 12% квартальная ставка составит 3%, соответственно показатели поквартального дисконтирования для i-го квартала составят (1 0,03) и независимо от условий выпуска («показатели дисконтирования »приведены в табл 64тування» наведені в табл. 6.4).

Таблица 64

дисконтированной стоимости процентных выплат за ТРЕМЯ объектами ИНВЕСТИРОВАНИЯ

Для 2-го квартала показатель дисконтирования равна (1 0,03) 2 =

= 1,0609, для 3-го - (1 0,03) 3 = 1,033 = 1,092727 и т д

Абсолютная сумма ежеквартальных процентных выплат для первого варианта (20% годовых) составит: 10 000,00 • 0,20 / 4 =

= 500,00 грн, для второго варианта (20,4% годовых) - ежегодная сумма процентов составит: 10 000,00 • 0,204 = 2 040,00 грн, для третьего варианта (22% годовых) абсолютная сумма процентов за два уплачиваемых при погашении, составляет 10 000,00? іантів у графу відповідного кварталу.

Три последние строки таблицы 4 содержат дисконтированные суммы процентных выплат как частное от деления абсолютной суммы на соответствующий показатель дисконтирования Например, для 4-го квартала показатель дисконтув ния составляет 1,125509, поэтому для варианта ежеквартальных выплат дисконтированная на четыре квартала стоимость процентных выплат в 500,00 грн составит 500,00 / 1,125509 = 444,24 декабрьн. Суммарный дисконтированный денежный поток (сумма стоимости погашения и всех процентных выплат) на дату анализа по каждому из вариантов инвестирования (вложений) приведем в табл 65:

Таблица 65

СУММАРНЫЙ дисконтированных денежных ПОТОК (ДГП) НА ДАТУ АНАЛИЗА ПО КАЖДОМУ ИЗ ТРЕХ ВАРИАНТОВ ИНВЕСТИРОВАНИЯ (вложений)

Поскольку погашение во всех трех вариантах состоится через восемь кварталов, значение в графе 3 табл 65 определяется через дисконтирование суммы погашения (10 000,00 грн) на показатель дисконтирования (1 0,03) 8 = 1,266770,03)8 = 1,266770:

Данные графы 4 является итогом с 1-го по 8-й квартал (табл 64) показателей дисконтирования Так, по варианту а) 485,44 471,30

457,57 444,24 431,30 418,74 406,55 394,70 = 3509,85;

по варианту б) 1866,89 1658,71 = 3525,60;

по варианту в) 3473,40

Суммарное значение дисконтированных процентных выплат приведен в графе 4, а сумма графы 3 и графы 4 приведена в графе 5 Разделив полученные значения на сумму вложения (номинал, равный 10 000,00 грн), в получим доходность по каждому из вариантов Итак, если взять ставку дисконтирования 12,0%, приходим к выводу, что, учитывая периодичность уплаты процентных доходов и анализ их дисконтированной стоимости, эффективным является вариант б (вложения с номинальной доходностью 20,4% годовых и ежегодной выплатой процентов), а вариант с номинальной доходностью 22,0% является наихудшим с точки зрения эффективной (дисконтированная ной) доходности (дисконтованої) дохідності.